mo1
1. Что такое объект, целевая переменная, признак, модель, функционал ошибки и обучение?
Объект – некая абстрактная сущность, с которой мы хотим работать и для которой хотим делать предсказания.
Пространство объектов – множество всех возможных объектов в данной задаче. Целевая переменная – некая характеристика объекта, которую мы хотим научиться предсказывать с помощью методов машинного обучения. Обычно объект обозначается \(x\), пространство объектов - \(\mathbb{X}\). Целевая переменная обозначается - \(y\), пространство ответов - \(\mathbb{Y}\).
Объекты описываются с помощью своих характеристик, называемых признаками (т.е. признак – некая характеристика объекта), вектор признаков является признаковым описанием объекта. Мы будем отождествлять объект и его признаковое описание. Модель – некоторый алгоритм, позволяющий предсказывать целевую переменную по признаковому описанию объекта. По сути, это функция \(a: \mathbb{X} \to \mathbb{Y}\).
Функционал качества позволяет оценить качество работы такого алгоритма, при этом, если функционал устроен так, что его нужно минимизировать, будем называть его функционалом ошибки. Функционал обозначается \(Q(a, X)\) и чаще всего представляет собой сумму ошибок на отдельных объектах, а функция, измеряющая ошибку на одном объекте, называется функцией потерь.
Пусть нам дано множество объектов \(\mathbb{X}\) - матрица объекты-признаки - с известными ответами \(\mathbb{Y}\). Назовем совокупность (\(\mathbb{X}\), \(\mathbb{Y}\)) обучающей выборкой. Обучением будем называть процесс построения оптимального с точки зрения функционала ошибки на обучающей выборке алгоритма \(a\).
2. Запишите формулы для линейной модели регрессии и для среднеквадратичной ошибки. Запишите среднеквадратичную ошибку в матричном виде.
Линейная модель:
\[ \mathbb{A} = \{ a(x) = w_0 + w_1 x_1 + \dots + w_d x_d|w_0, w_1, \dots, w_d \in \mathbb{R} \} \], где через \(x_i\) обозначается значение \(i\) -го признака у объекта \(x\), a \(d\) – количество объектов, \(w_{i}\) – вес для $i$-го признака.
MSE:
В общем виде
\[ Q(a,X)=\frac{1}{\ell}\sum_{i=1}^{\ell}(a(x_{i})-y_{i})^{2} \], где \(a(x)\) – модель, \(l\) – количество объектов.
Для некой модели \(a(x)\) описанной выше
\[ \frac{1}{\ell}\sum_{i = 1}^{\ell} \left(w_0+\sum_{j = 1}^{d}w_j x_{ij}-y_i\right)^2\to\min_{w_0, w_1,\dots, w_d}. \]
В матричном виде
\[ \frac{1}{\ell}||Xw-y||^{2}_{2}\to \min_{w} \] \[ Q(w)=(y-Xw)^{T}(y-Xw) \] где \(X\) - матрица объекты-признаки, \(w\) - вектор весов, \(y\) - вектор целевых значений,\(||x||^{2}_{2}\) - L2 норма (квадратный корень из суммы квадратов значений вектора)
3. Что такое коэффициент детерминации? Как интерпретировать его значения?
\[ R^{2}(a,X)=1-\frac{\sum_{i=1}^{l}(a(x_{i}-y_{i})^{2})}{\sum_{i=1}^{l}(y_{i}-\hat{y})^{2}} \] Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
4. Чем отличаются функционалы MSE и MAE?
- MAE более устойчива к выбросам (но гораздо менее точна при приближении к минимуму (произв не содержит инф о близости к экстремуму (в 0 вообще ее нет)) и большим значениям
- MSE увеличит ошибку из-за возведения в квадрат из-за чего появится некоторое искажение реальной ошибки. Если выбросов больше чем нормальных объектов, то устойчивость MAE пропадает.
5. Как устроены робастные функции потерь (Huber loss, log-cosh)? Чем log-cosh лучше функции потерь Хубера?
Huber loss
Huber Loss объединяет в себе MSE и MAE с параметром дельта, этот параметр определяет, что мы считаем за выброс. При \(\delta\rightarrow0\) функция потерь Хубера вырождается в абсолютную функцию (MAE) потерь, а при \(\delta\rightarrow\infty\) - в квадратичную (MSE). Не имеет вторую производную
\[ L_\delta(y, a)= \left\{\begin{aligned} &\frac12 (y - a)^2, \quad |y - a| < \delta \\ &\delta \left(|y - a| - \frac12 \delta \right), \quad |y - a| \geq \delta \end{aligned} \right. \]
Log Cosh
Log Cosh (логарифм от гиперболического косинуса) имеет вторую производную. Как и в случае с функцией потерь Хубера, для маленьких отклонений здесь имеет место квадратичное поведение, а для больших - линейное. \[ L(y,a)=\log(\cosh(a-y)) \]
Сравнение
Log Cosh > Huber Loss т.к. Вторая производная в Хубере имеет разрывы, Log Cosh же без разрывов, не нужно подбирать параметр дельта.
6. Что такое градиент? Какое его свойство используется при минимизации функций?
Градиент - направление наискорейшего роста функции, а антиградиент (т.е. \(−\nabla f\) ) направлением наискорейшего убывания функции. Это ключевое свойство градиента, обосновывающее его использование в методах оптимизации.
7. Как устроен градиентный спуск?
Пусть \(w^0\) начальный набор параметров (например, нулевой или сгенерированный из некоторого случайного распределения). Тогда градиентный спуск состоит в повторении следующих шагов до сходимости: \[ w^{(k)}=w^{(k - 1)}-\eta_k\nabla Q(w^{(k - 1)}) \] Здесь под \(Q(w)\) понимается значение функционала ошибки для набора параметров \(w\).
Через \(\eta_k\) обозначается длина шага, которая нужна для контроля скорости движения. Можно делать её константной: \(\eta_k = c\). При этом если длина шага слишком большая, то есть риск постоянно <перепрыгивать> через точку минимума, а если шаг слишком маленький, то движение к минимуму может занять слишком много итераций. Иногда длину шага монотонно уменьшают по мере движения - например, по простой формуле (\(\frac{1}{k}\)).
8. Почему не всегда можно использовать полный градиентный спуск? Какие способы оценивания градиента вы знаете? Почему в стохастическом градиентном спуске важно менять длину шага по мере итераций? Какие стратегии изменения шага вы знаете?
Использование полного градиентного спуска может быть очень трудоёмко при больших размерах выборки. В то же время точное вычисление градиента может быть не так уж необходимо - как правило, мы делаем не очень большие шаги в сторону антиградиента, и наличие в нём неточностей не должно сильно сказаться на общей траектории. Опишем несколько способов оценивания полного градиента.
SGD
\[ w^{(k)}=w^{(k - 1)}-\eta_k\nabla q_{ik}(w^{(k - 1)}) \] где \(i_k\) – случайно выбранный номер слагаемого из функционала. Параметры, оптимальные для средней ошибки на всей выборке, не обязаны являться оптимальными для ошибки на одном из объектов. Поэтому SGD метод запросто может отдаляться от минимума, даже оказавшись рядом с ним. Чтобы исправить эту проблему, важно в SGD делать длину шага убывающей – тогда в окрестности оптимума мы уже не сможем делать длинные шаги и, как следствие, не сможем из этой окрестности выйти. Разумеется, потребуется выбирать формулу для длины шага аккуратно, чтобы не остановиться слишком рано и не уйти от минимума. В частности, сходимость для выпуклых дифференцируемых функций гарантируется (с вероятностью 1), если функционал удовлетворяет ряду условий (как правило, это выпуклость, дифференцируемость и липшицевость градиента) и длина шага удовлетворяет условиям Роббинса-Монро: \[ \sum_{k = 1}^{\infty} \eta_k = \infty; \quad \sum_{k = 1}^{\infty} \eta_k^2 < \infty. \] Этим условиям, например, удовлетворяет шаг \(\eta_k = \frac{1}{k}\).
Примеры использования
\(\eta_{k}=\frac{1}{k}\) \(\eta_{k}=\lambda(\frac{s_{0}}{s_{0}+k})^{p}\)
SAG
На \(k\) -й итерации выбирается случайное слагаемое \(i_{k}\) и обновляются вспомогательные переменные: \[ z_i^{(k)} = \begin{cases} \nabla q_i(w^{(k - 1)}), \quad &\text{если}\ i = i_k;\\ z_i^{(k - 1)} \quad &\text{иначе}. \end{cases}\] \[ w^{(k)}=w^{(k - 1)}-\eta_k\frac{1}{\ell}\sum_{i = 1}^{\ell}z_i^{(k)} \]
9. В чём заключаются метод инерции и AdaGrad/RMSProp?
Adagrad
В методе AdaGrad предлагается сделать свою длину шага для каждой компоненты вектора параметров. При этом шаг будет тем меньше, чем более длинные шаги мы делали на предыдущих итерациях \[ G_{kj} = G_{k-1,j} + (\nabla_w Q(w^{(k-1)}))_j^2 \] \[ w_j^{(k)} = w_j^{(k-1)} - \frac{\eta_t}{\sqrt{G_{kj} + \varepsilon}} (\nabla_w Q(w^{(k-1)}))_j \] недостаток: переменная \(G_{kj}\) монотонно растёт, из-за чего шаги становятся всё медленнее и могут остановиться ещё до того, как достигнут минимум функционала
RMSprop
Улучшение над AdaGrad. В этом случае размер шага по координате зависит в основном от того, насколько быстро мы двигались по ней на последних итерациях \[G_{kj} = \alpha G_{k-1,j} + (1 - \alpha) (\nabla_w Q(w^{(k-1)}))_j^2.\]
10. Что такое кросс-валидация? На что влияет количество блоков в кросс-валидации? Как построить итоговую модель после того, как по кросс-валидации подобраны оптимальные гиперпараметры?
- CV – размеченные данные разбиваются на \(k\) блоков примерно одинакового размера. Затем обучается \(k\) моделей \(a_1(x), \dots, a_k(x)\) причём \(i\) -я модель обучается на объектах из всех блоков, кроме блока \(i\). После этого качество каждой модели оценивается по тому блоку, который не участвовал в её обучении, и результаты усредняются: \[\text{CV} = \frac{1}{k} \sum_{i = 1}^{k} Q\left( a_i(x), X_i \right).\]
- можно построить композицию из моделей \(a_1(x), \dots, a_k(x)\), полученных в процессе кросс-валидации. Под композицией может пониматься, например, усреднение прогнозов этих моделей, если мы решаем задачу регрессии.
11. Чем гиперпараметры отличаются от параметров? Что является параметрами и гиперпараметрами в линейных моделях и в решающих деревьях?
- Параметры - величины, которые настраиваются по обучающей выборке
- Гиперпараметры - относят величины, которые контролируют сам процесс обучения и не могут быть подобраны по обучающей выборке
- Параметры для линейных моделей:
- Веса
- Гиперпараметр для линейных моделей:
- Коэффициент регуляризации
- Размер шага градиента
- Параметр для деревьев:
- Разбиение
- Гиперпараметр для деревьев:
- Глубина дерева
- Минимальное количество элементов в листьях
- Минимальное количество элементов для разбиения
12. Что такое регуляризация? Запишите L1- и L2-регуляризаторы.
Регуляризация – способ штрафовать модель за высокую норму весов с помощью коэффициента регуляризации для предотвращения переобучения. Наиболее распространенными являются \(L_2\) и \(L_1\) -регуляризаторы: \[ R(w) = \|w\|_2 = \sum_{i = 1}^d w_i^2, \] \[ R(w) = \|w\|_1 = \sum_{i = 1}^d |w_i|. \]
13. Почему L1-регуляризация отбирает признаки?
Зануление весов
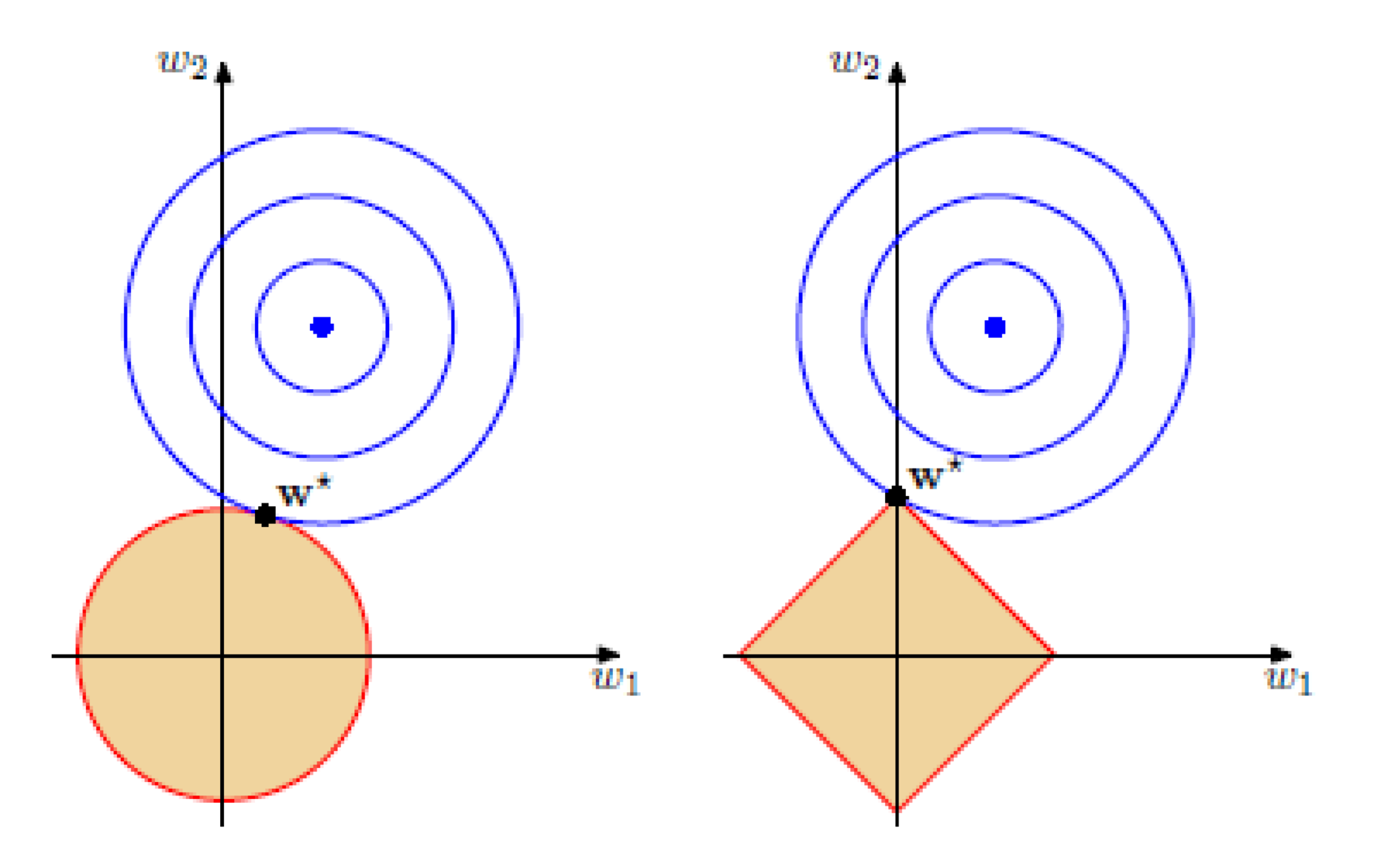
Можно показать, что если функционал \(Q(w)\) является выпуклым, то задача безусловной минимизации функции \(Q(w) + \alpha \|w\|_1\) эквивалентна задаче условной оптимизации \[Q(w) \to \min_{w}\] \[\|w\|_1 \leq C\] для некоторого \(C\). Изображены линии уровня функционала \(Q(w)\), а также множество, определяемое ограничением \(\|w\|_1 \leq C\). Решение определяется точкой пересечения допустимого множества с линией уровня, ближайшей к безусловному минимуму. Из изображения можно предположить, что в большинстве случаев эта точка будет лежать на одной из вершин ромба, что соответствует решению с одной зануленной компонентой.
Штрафы при малых весах
Предположим, что текущий вектор весов состоит из двух элементов \(w = (1, \varepsilon)\), где \(\varepsilon\) близко к нулю, и мы хотим немного изменить данный вектор по одной из координат. Найдём изменение \(L_2\) - и \(L_1\) -норм вектора при уменьшении первой компоненты на некоторое положительное число \(\delta < \varepsilon\): \[\|w - (\delta, 0)\|_2^2=1 - 2 \delta + \delta^2 + \varepsilon^2\] \[\|w - (\delta, 0)\|_1=1 - \delta + \varepsilon\] Вычислим то же самое для изменения второй компоненты: \[\|w - (0, \delta)\|_2^2=1 - 2 \varepsilon \delta + \delta^2 + \varepsilon^2\] \[\|w - (0, \delta)\|_1 =1 - \delta + \varepsilon\] Видно, что с точки зрения \(L_2\) -нормы выгоднее уменьшать первую компоненту, а для \(L_1\) -нормы оба изменения равноценны. Таким образом, при выборе \(L_2\) -регуляризации гораздо меньше шансов, что маленькие веса будут окончательно обнулены.
Проксимальный шаг
Проксимальные методы – это класс методов оптимизации, которые хорошо подходят для функционалов с негладкими слагаемыми. Формула для шага проксимального метода в применении к линейной регрессии с квадратичным функционалом ошибки и \(L_1\) -регуляризатором: \[w^{(k)}=S_{\eta \alpha} \left(w^{(k - 1)}-\eta\nabla_w F(w^{(k - 1)})\right),\] где \(F(w) = \|Xw - y\|^2\) – функционал ошибки без регуляризатора, \(\eta\) – длина шага, \(\alpha\) – коэффициент регуляризации, а функция \(S_{\eta \alpha}(w)\) применяется к вектору весов покомпонентно, и для одного элемента выглядит как \[S_{\eta \alpha} (w_i)= \begin{cases} w_i - \eta \alpha, \quad &w_i > \eta \alpha\\ 0, \qquad &|w_i| < \eta \alpha\\ w_i + \eta \alpha, \quad &w_i < -\eta \alpha \end{cases}\] Из формулы видно, что если на данном шаге значение некоторого веса не очень большое, то на следующем шаге этот вес будет обнулён, причём чем больше коэффициент регуляризации, тем больше весов будут обнуляться.
14. Почему плохо накладывать регуляризацию на свободный коэффициент? Почему регуляризация может странно работать на немасштабированных данных?
Отметим, что свободный коэффициент \(w_0\) нет смысла регуляризовывать - если мы будем штрафовать за его величину, то получится, что мы учитываем некие априорные представления о близости целевой переменной к нулю и отсутствии необходимости в учёте её смещения. Такое предположение является достаточно странным. Особенно об этом следует помнить, если в выборке есть константный признак и коэффициент \(w_0\) обучается наряду с остальными весами; в этом случае следует исключить слагаемое, соответствующее константному признаку, из регуляризатора.
Может быть большой разброс порядков весов.
15. Запишите формулу для линейной модели классификации. Что такое отступ? Как обучаются линейные классификаторы и для чего нужны верхние оценки пороговой функции потерь?
Формула
\[ a(x) = \text{sign}\left( \langle w, x \rangle + w_0 \right) = \text{sign} \left( \sum_{j = 1}^{d} w_j x_j + w_0 \right) \]
Отступ
\[ M_i = y<w,x_i> \] Знак отступа говорит о корректности ответа классификатора (положительный отступ соответствует правильному ответу, отрицательный неправильному), а его абсолютная величина характеризует степень уверенности классификатора в своём ответе. Напомним, что скалярное произведение \(<w,x_i>\) пропорционально расстоянию от разделяющей гиперплоскости до объекта; соответственно, чем ближе отступ к нулю, тем ближе объект к границе классов, тем ниже уверенность в его принадлежности.
Обучение линейных классификаторов
Нам будет удобнее решать задачу минимизации, поэтому будем вместо этого использовать долю неправильных ответов \[ Q(a, X)= \frac{1}{\ell} \sum_{i = 1}^{\ell} [a(x_i) \neq y_i] = \frac{1}{\ell} \sum_{i = 1}^{\ell} [\mathop{\rm sign}\limits \langle w, x_i \rangle \neq y_i] \to \min_w \] Этот функционал является дискретным относительно весов, и поэтому искать его минимум с помощью градиентных методов мы не сможем. Более того, у данного функционала может быть много глобальных минимумов вполне может оказаться, что существует много способов добиться оптимального количества ошибок. Чтобы не пытаться решать все эти проблемы, попытаемся свести задачу к минимизации гладкого функционала (верхней оценки).
Верхние оценки
Функционал оценивает ошибку алгоритма на объекте \(x\) с помощью пороговой функции потерь \(L(M) = [M < 0]\),
где аргументом функции является отступ \(M = y \langle w, x \rangle\). Оценим эту функцию сверху во всех точках \(M\) кроме, может быть, небольшой полуокрестности левее нуля:\[
L(M) \leq \tilde L(M).
\]
После этого можно получить верхнюю оценку на функционал:
\[
Q(a, X)
\leq
\frac{1}{\ell}
\sum_{i = 1}^{\ell}
\tilde L(y_i \langle w, x_i \rangle)
\to
\min_w
\]
Если верхняя оценка \(\tilde L(M)\) является гладкой, то и данная верхняя оценка будет гладкой. В этом случае её можно будет минимизировать с помощью, например, градиентного спуска. Если верхнюю оценку удастся приблизить к нулю, то и доля неправильных ответов тоже будет близка к нулю.
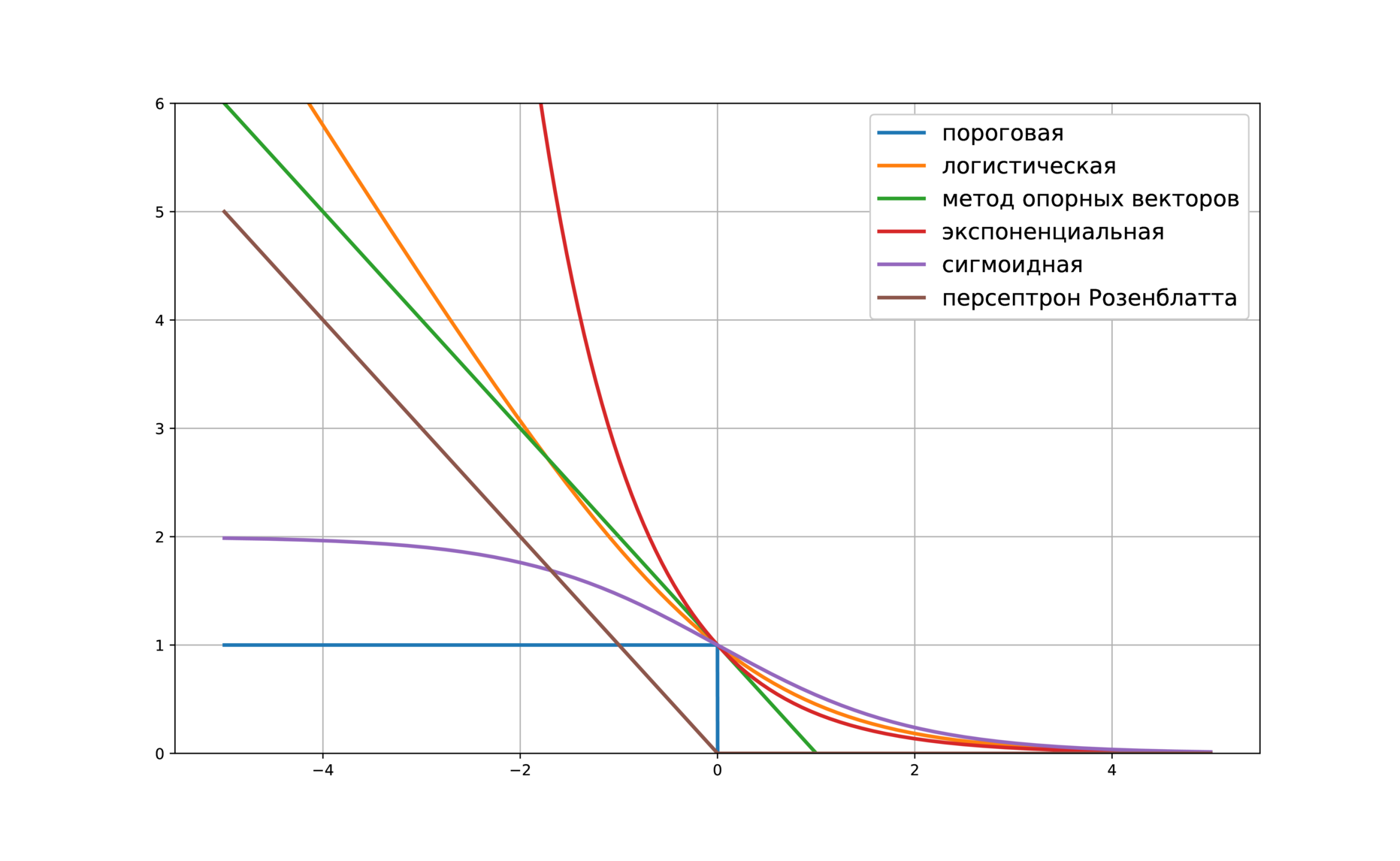 Приведём несколько примеров верхних оценок:
Приведём несколько примеров верхних оценок:
- \(\tilde L(M) = \log \left(1 + e^{-M} \right)\) – логистическая функция потерь
- \(\tilde L(M) = (1 - M)_+ = \max(0, 1 - M)\) – кусочно-линейная функция потерь (используется в методе опорных векторов)
- \(\tilde L(M) = (-M)_+ = \max(0, -M)\) – кусочно-линейная функция потерь (соответствует персептрону Розенблатта)
- \(\tilde L(M) = e^{-M}\) – экспоненциальная функция потерь
- \(\tilde L(M) = 2/(1 + e^M)\) – сигмоидная функция потерь
Любая из них подойдёт для обучения линейного классификатора.
16. Что такое точность, полнота и F-мера? Почему F-мера лучше арифметического среднего и минимума?
| y=1 | y=-1 | |
|---|---|---|
| a(x)=1 | True Positive (TP) | False Positive (FP) |
| a(x)=-1 | False Negative (FN) | True Negative (TN) |
Точность
Точность (которая не accuracy (которой точный перевод - доля верных ответов), а precision) - метрика того, насколько можно доверять модели если она сказала что объект относится к положительному классу. \[ \text{precision}=\frac{\text{TP}}{\text{TP} + \text{FP}} \]
Полнота
Полнота (recall) - метрика того, насколько хорошо модель покрыла положительный класс \[ \text{recall}=\frac{\text{TP}}{\text{TP} + \text{FN}} \]
F-мера
F - мера - гармоническое среднее точности и полноты, (сохраняет хорошее от ариф. минимума, но более гладкая. Близко к 0 если хотя бы 1 из аргументов близок к нулю). В отличие от геометрического среднего - гармоническое среднее гораздо устойчивее к выбросам. \[ F=\frac{2 * \text{precision} * \text{recall}}{\text{precision} + \text{recall}} \]
17. Для чего нужен порог в линейном классификаторе? Из каких соображений он может выбираться?
- Для определения класса объекта
- Может выбираться:
- из цен ошибок
- из требуемого количества
- из требований к recall и precision
18. Что такое AUC-ROC? Опишите алгоритм построения ROC-кривой.
AUC ROC-area under ROC (receiving operating characteristic) curve, - площадь под ROC-кривой. Сортируем объекты \(b(x)\), по размеру порога; размер шага для объектов с \([y = 0] =\frac{1}{L_{-}}\) отрицательных (шаги по FPR (горизонт ось)), шаги для \([y = 1] =\frac{1}{L_+}\) положительных (шаги по TPR (верт ось) )
19. Что такое AUC-PRC? Опишите алгоритм построения PR-кривой.
Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (AUC-PR).
Описание алгоритма
Стартуем из точки (0, 1). Будем идти по ранжированной выборке, начиная с первого объекта; пусть текущий объект находится на позиции \(k\). Если он относится к классу −1, то полнота не меняется, точность падает соответственно, кривая опускается строго вниз на \(\frac{1}{l_{-}}\). Если же объект относится к классу 1, то полнота увеличивается на \(\frac{1}{l_+}\), точность растет, и кривая поднимается вправо и вверх. Площадь под этим участком можно аппроксимировать площадью прямоугольника с высотой, равной precision@k и шириной \(\frac{1}{l_{+}}\).
20. Что означает “модель оценивает вероятность положительного класса”? Как можно внедрить это требование в процедуру обучения модели?
Рассмотрим точку \(x\) пространства объектов. Как мы договорились, в ней имеется распределение на ответах \(p(y = +1 | x)\). Допустим, алгоритм \(b(x)\) возвращает числа из отрезка \([0, 1]\). Наша задача – выбрать для него такую процедуру обучения, что в точке \(x\) ему будет оптимально выдавать число \(p(y = +1 | x)\). Если в выборке объект \(x\) встречается \(n\) раз с ответами \(\{y_1, \dots, y_n\}\), то получаем следующее требование: \[ \mathop{\rm arg\,min}\limits_{b \in \mathbb{R}} \frac{1}{n} \sum_{i = 1}^{n} L(y_i, b) \approx p(y = +1 | x) \] При стремлении \(n\) к бесконечности получим, что функционал стремится к матожиданию ошибки: \[ \mathop{\rm arg\,min}\limits_{b \in \mathbb{R}}\mathbb{E} \left[L(y, b)|x\right] = p(y = +1 | x) \] На семинаре будет показано, что этим свойством обладает, например, квадратичная функция потерь \(L(y, z) = (y - z)^2\), если в ней для положительных объектов использовать истинную метку \(y = 1\), а для отрицательных брать \(y = 0\). Если функция потерь \(L\) удовлетворяет второй формуле, то \(b(x)\approx p(y=+1|x)\)
21. Что такое калибровочная кривая? Какие методы калибровки вероятности вы знаете? Почему важно проводить калибровку не на обучающей выборке?
Калибровка вероятностей нужна для того, чтобы заставить модель выдавать корректные вероятности принадлежности к классам. В задаче бинарной классификации откалиброванным алгоритмом называют такой алгоритм, для которого доля положительных примеров (на основе реальных меток классов) для предсказаний в окрестности произвольной вероятности \(p\) совпадает с этим значением \(p\). На этой кривой абсцисса точки соответствуют значению \(p\) (предсказаний алгоритма), а ордината соответствует доле положительных примеров, для которых алгоритм предсказал вероятность, близкую к \(p\). В идеальном случае эта кривая совпадает с прямой \(y = x\). Есть два подхода к калибровке.
- Масштабирование Платта. Он заключается к подгонке всех предсказаний к логистической кривой (по сути, логистическая регрессия на ответах классификатора) \[P(y = 1 | x) = \frac{1}{1+\exp (af(x) + b)},\] где \(a, b\) – скалярные параметры. Эти параметры настраиваются методом максимума правдоподобия (минимизируя логистическую функцию потерь) на отложенной выборке или с помощью кросс валидации. Также Платт предложил настраивать параметры на обучающей выборке базовой модели, а для избежания переобучения изменить метки объектов на следующие значения:
- \[t_{+} = \frac{N_{+} + 1}{N_{-} + 2}\] для положительных примеров
- \[t_{-} = \frac{1}{N_{-} + 2}\] для отрицательных.
- Изотоническая регрессия. В этом методе также строится отображение из предсказаний модели в откалиброванные вероятности. Для этого используем изотоническую функцию (неубывающая кусочно-постоянная функция), в которой \(x\) – выходы нашего алгоритма, а \(y\) – целевая переменная. Мы хотим найти такую функцию \(m(t)\): \(P(y = 1 | x) = m(f(x))\). Она настраивается под квадратичную ошибку: \[m = \mathop{\rm arg\,min}\limits_{z} \sum (y_i - z(f(x_i))^2,\] с помощью специального алгоритма (Pool-Adjacent-Violators Algorithm). В результате калибровки получаем надстройку над нашей моделью, которая применяется поверх предсказаний базовой модели.
22. Запишите функционал логистической регрессии. Как он связан с методом максимума правдоподобия?
Модель: \[ p(y = 1| x) = \frac{1}{1 + \exp(-\langle w, x \rangle)}. \] Подставим трансформированный ответ линейной модели в логарифмическую функцию потерь: \[ -\sum_{i = 1}^{\ell}\left([y_i = +1] \log \frac{1}{1 + \exp(-\langle w, x_i \rangle)} +[y_i = -1]\log \frac{\exp(-\langle w, x_i \rangle)}{1 + \exp(-\langle w, x_i \rangle)} \right) = -\sum_{i = 1}^{\ell} \left( [y_i = +1]\log \frac{1}{1 + \exp(-\langle w, x_i \rangle)} +[y_i = -1]\log \frac{1}{1 + \exp(\langle w, x_i \rangle)} \right) = \sum_{i = 1}^{\ell} \log \left( 1 + \exp(-y_i \langle w, x_i \rangle) \right). \]
Попробуем сконструировать функцию потерь из других соображений. Если алгоритм \(b(x) \in [0, 1]\) действительно выдает вероятности, то они должны согласовываться с выборкой. С точки зрения алгоритма вероятность того, что в выборке встретится объект \(x_i\) с классом \(y_i\), равна \(b(x_i)^{[y_i = +1]} (1 - b(x_i))^{[y_i = -1]}\). Исходя из этого, можно записать правдоподобие выборки (т.е. вероятность получить такую выборку с точки зрения алгоритма): \[ Q(a, X)= \prod_{i = 1}^{\ell} b(x_i)^{[y_i = +1]} (1 - b(x_i))^{[y_i = -1]}. \] Данное правдоподобие можно использовать как функционал для обучения алгоритма – с той лишь оговоркой, что удобнее оптимизировать его логарифм:\[-\sum_{i = 1}^{\ell} \left([y_i = +1] \log b(x_i) + [y_i = -1] \log (1 - b(x_i))\right) \to\min \]
23. Запишите задачу метода опорных векторов для линейно неразделимого случая. Как функционал этой задачи связан с отступом классификатора? Как выглядит задача безусловной оптимизации в SVM?
Условный
\[ \left\{\begin{aligned} & \frac{1}{2} \|w\|^2 + C \sum_{i = 1}^{\ell} \xi_i \to \min_{w, b, \xi} \\ & y_i \left( \langle w, x_i \rangle + b \right) \geq 1 - \xi_i, \quad i = 1, \dots, \ell, \\ & \xi_i \geq 0, \quad i = 1, \dots, \ell. \end{aligned} \right. \]
Безусловный
\[
\frac12 \|w\|^2+
C
\sum_{i = 1}^{\ell}
\max(0,
1 - y_i (\langle w, x_i \rangle + b))
\to
\min_{w, b}
\]
Величина \(\frac{1}{\|w\|}\) в данном случае называется мягким отступом (soft margin). С одной стороны, мы хотим максимизировать отступ, с другой – минимизировать штраф за неидеальное разделение выборки \(\sum_{i = 1}^{\ell} \xi_i\).
24. В чём заключаются one-vs-all и all-vs-all подходы в многоклассовой классификации?
One-vs-all
Обучим \(K\) линейных классификаторов \(b_1(x), \dots, b_K(x)\), выдающих оценки принадлежности классам \(1, \dots, K\) соответственно. Например, в случае с линейными моделями эти модели будут иметь вид \(b_k(x) = \langle w_k, x \rangle + w_{0k}\). Классификатор с номером \(k\) будем обучать по выборке \(\left(x_i, 2 [y_i = k] - 1\right)_{i = 1}^{\ell}\); иными словами, мы учим классификатор отличать \(k\) -й класс от всех остальных.
Итоговый классификатор будет выдавать класс, соответствующий самому уверенному из бинарных алгоритмов: \[ a(x) = \mathop{\rm arg\,max}\limits_{k \in \{1, \dots, K\}} b_k(x). \]
Проблема данного подхода заключается в том, что каждый из классификаторов \(b_1(x), \dots, b_K(x)\) обучается на своей выборке, и выходы этих классификаторов могут иметь разные масштабы, из-за чего сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением – так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
All-vs-all
Обучим \(C_K^2\) классификаторов \(a_{ij}(x)\), \(i, j = 1, \dots, K\), \(i \neq j\). Например, в случае с линейными моделями эти модели будут иметь вид \[ b_k(x) = \mathop{\rm sign}\limits(\langle w_k, x \rangle + w_{0k} ). \] Классификатор \(a_{ij}(x)\) будем настраивать по подвыборк \(X_{ij} \subset X\), содержащей только объекты классов \(i\) и \(j\): \[ X_{ij} = \{(x_n, y_n) \in X | [y_n = i] = 1 \ \text{или}\ [y_n = j] = 1 \}. \] Соответственно, классификатор \(a_{ij}(x)\) будет выдавать для любого объекта либо класс \(i\), либо класс \(j\).
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов: \[ a(x) = \mathop{\rm arg\,max}\limits_{k \in \{1, \dots, K\}} \sum_{i = 1}^{K} \sum_{j \neq i} [a_{ij}(x) = k]. \]
25. Как измеряется качество в задаче многоклассовой классификации? Что такое микро- и макро-усреднение?
В многоклассовых задачах, как правило, стараются свести подсчет качества к вычислению одной из двухклассовых метрик. Выделяют два подхода к такому сведению: микро- и макро-усреднение.
Пусть выборка состоит из \(K\) классов. Рассмотрим \(K\) двухклассовых задач, каждая из которых заключается в отделении своего класса от остальных, то есть целевые значения для \(k\) -й задаче вычисляются как \(y_i^k = [y_i = k]\). Для каждой из них можно вычислить различные характеристики (TP, FP, и т.д.) алгоритма \(a^k(x) = [a(x) = k]\); будем обозначать эти величины как \(\text{TP}_k, \text{FP}_k, \text{FN}_k, \text{TN}_k\). Заметим, что в двухклассовом случае все метрики качества, которые мы изучали, выражались через эти элементы матрицы ошибок.
Микро-усренднение
При микро-усреднении сначала эти характеристики усредняются по всем классам, а затем вычисляется итоговая двухклассовая метрика – например, точность, полнота или F-мера. Например, точность будет вычисляться по формуле \[ \text{precision}(a, X) = \frac{\overline{\text{TP}}}{\overline{\text{TP}}+\overline{\text{FP}}}, \] где, например, \(\overline{\text{TP}}\) вычисляется по формуле \[ \overline{\text{TP}} = \frac{1}{K} \sum_{k = 1}^{K} \text{TP}_k. \]
Макро-усреднение
При макро-усреднении сначала вычисляется итоговая метрика для каждого класса, а затем результаты усредняются по всем классам. Например, точность будет вычислена как \[\text{precision}(a, X)=\frac{1}{K}\sum_{k = 1}^{K}\text{precision}_k(a, X);\qquad\] \[ \text{precision}_k(a, X)=\frac{\text{TP}_k}{\text{TP}_k+\text{FP}_k}. \]
Сравнение
Если какой-то класс имеет очень маленькую мощность, то при микро-усреднении он практически никак не будет влиять на результат, поскольку его вклад в средние TP, FP, FN и TN будет незначителен. В случае же с макро-вариантом усреднение проводится для величин, которые уже не чувствительны к соотношению размеров классов (если мы используем, например, точность или полноту), и поэтому каждый класс внесет равный вклад в итоговую метрику.
26. В чём заключается преобразование категориальных признаков в вещественные с помощью mean-target encoding? Почему использование этого способа кодирования может привести к переобучению? Какие методы борьбы с этой проблемой вам известны?
Mean target encoding
Более сложный метод кодирования категориальных признаков – через целевую переменную. Идея в том, что алгоритму для предсказания цены необходимо знать не конкретный цвет автомобиля, а то, как этот цвет сказывается на цене. Разберём сначала базовый подход – mean target encoding (иногда его называют ).
Заменим каждую категорию на среднее значение целевой переменной по всем объектам этой категории. Пусть \(j\) -й признак является категориальным. Для бинарной классификации новый признак будет выглядеть следующим образом: \[ g_j(x, X) = \frac{ \sum_{i=1}^{\ell} [f_j(x) = f_j(x_i)][y_i = +1] }{ \sum_{i=1}^{\ell} [f_j(x) = f_j(x_i)] }, \] где \(f_j(x_i)\) – \(j\) -й признак \(i\) -го объекта, \(y_i\) – класс \(i\) -го объекта.
Отметим, что эту формулу легко перенести как на случай многоклассовой классификации (в этом случае будем считать \(K\) признаков, по одному для каждого класса, и в числителе будет подсчитывать долю объектов с заданной категорией и с заданным классом), так и на случай регрессии (будем вычислять среднее значение целевой переменной среди объектов данной категории).
Вернёмся к бинарной классификации. Можно заметить, что для редких категорий мы получим некорректные средние значения целевой переменной. Например, в выборке было только три золотистых автомобиля, которые оказались старыми и дешёвыми. Из-за этого наш алгоритм начнёт считать золотистый цвет дешёвым. Для исправления этой проблемы можно регуляризировать признак средним значением целевой переменной по всем категориям так, чтобы у редких категорий значение было близко к среднему по всей выборке, а для популярных к среднему значению по категории. Формально для задачи бинарной классификации это выражается так: \[ g_j(x, X) = \frac{ \sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)][y_i = +1]+ \frac{C}{\ell}\sum_{i=1}^{\ell}[y_i = +1] }{ \sum_{i=1}^{\ell} [f_j(x) = f_j(x_i)] + C }, \] где \(C\) – коэффициент, отвечающий за баланс между средним значением по категории и глобальным средним значением.
Однако если мы вычислим значения \(g_j(x, X)\) по всей выборке, то столкнёмся с переобучением, так как мы внесли информацию о целевой переменной в признаки (новый признак слабая, но модель, предсказывающая целевое значение). Поэтому вычисление таких признаков следует производить по блокам, то есть вычислять средние значения на основе одних фолдов для заполнения на другом блоке (аналогично процессу кросс-валидации). Если же ещё планируется оценка качества модели с помощью кросс-валидации по блокам, то придётся применить для подсчёта признаков. Этот подход заключается в кодировании категориальных признаков по блокам внутри блоков, по которым оценивается качество модели.
Разберём этот процесс. Представим, что хотим посчитать качество модели на 3-м блоке. Для этого:
- Разбиваем все внешние блоки, кроме 3-го, на внутренние блоки. Количество внутренних блоков может не совпадать с количеством внешних.
- Рассмотрим конкретный внешний Для каждого из его внутренних блоков считаем значение \(g(x, X)\) на основе средних значений целевой переменной по блокам, исключая текущий. Для 3-го внешнего блока (который сейчас играет роль тестовой выборки) вычисляем \(g(x, X)\) как среднее вычисленных признаков по каждому из внутренних фолдов.
- Обучаем модель на всех блоках, кроме 3-го, делаем предсказание на 3-м и считаем на нём качество.
Существуют альтернативы кодированию категориальных признаков по блокам.
Зашумление
Можно посчитать новые признаки по базовой формуле, а затем просто добавить к каждому значению случайный шум (например, нормальный). Это действительно снизит уровень корреляции счётчиков с целевой переменной. Проблема в том, что это делается за счёт снижения силы такого признака, а значит, мы ухудшаем итоговое качество модели. Поэтому важно подбирать дисперсию шума, чтобы соблюсти баланс между борьбой с переобучением и предсказательной силой счётчиков.
Сглаживание
Можно немного модифицировать формулу, чтобы сила регуляризации зависела от объёма данных по конкретной категории: \[ g_j(x, X) = \lambda \left( n(f_j(x)) \right) \frac{ \sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)][y_i = +1] }{ \sum_{i=1}^{\ell}[f_j(x) = f_j(x_i)] } +\left( 1 - \lambda \left( n(f_j(x)) \right) \right) \frac{1}{\ell} \sum_{i = 1}^{\ell} [y_i = +1] , \] где \(n(z) = \sum_{i = 1}^{\ell} [f_j(x_i) = z]\) – число объектов категории \(z\), \(\lambda(n)\) – некоторая монотонно возрастающая функция, дающая значения из отрезка \([0, 1]\). Примером может служить \(\lambda(n) = \frac{1}{1 + \exp(-n)}\). Если грамотно подобрать эту функцию, то она будет вычищать значение целевой переменной из редких категорий и мешать переобучению.
Кодирование по времени.
Можно отсортировать выборку некоторым образом и для \(i\) -го объекта вычислять статистики только по предыдущим объектам: \[ g_j(x_k, X) = \frac{ \sum_{i=1}^{k - 1} [f_j(x) = f_j(x_i)][y_i = +1] }{ \sum_{i=1}^{k - 1} [f_j(x) = f_j(x_i)] }. \] Для хорошего качества имеет смысл отсортировать выборку случайным образом несколько раз, и для каждого такого порядка посчитать свои счётчики. Это даёт улучшение качества, например, потому что для объектов, находящихся в начале выборки, признаки будут считаться по очень небольшой подвыборке, и поэтому вряд ли будут хорошо предсказывать целевую переменную. При наличии нескольких перестановок хотя бы один из новых признаков будет вычислен по подвыборке достаточного размера. Такой подход, например, используется в библиотеке CatBoost.
Weight of Evidence
Существует альтернативный способ кодирования категориальных признаков, основанный на подсчёте соотношения положительных и отрицательных объектов среди объектов данной категории. Этот подход, в отличие от других, сложнее обобщить на многоклассовый случай или для регрессии.
Введём обозначение для доли объектов класса \(b\) внутри заданной категории \(c\) среди всех объектов данного класса в выборке: \[ P(c | y = b)= \frac{ \sum_{i = 1}^{\ell}[y_i = b] [f_j(x_i) = c]+\alpha }{ \sum_{i = 1}^{\ell}[y_i = b]+2 \alpha }, \] где \(\alpha\) – параметр сглаживания. Вычислим новое значение признака как \[ g_j(x, X) = \log\left( \frac{ P(f_j(x) | y = +1) }{ P(f_j(x) | y = -1) } \right). \] Если \(g_j(x, X)\) близко к нулю, то данная категория примерно с одинаковой вероятностью встречается в обоих классах, и поэтому вряд ли будет хорошо предсказывать значение целевой переменной. Чем сильнее отличие от нуля, тем сильнее категория характеризует один из классов.
Разумеется, в конкретной задаче лучше всего может себя проявлять любой из этих подходов, поэтому имеет смысл сравнивать их и выбирать лучший – или использовать все сразу.
27. Как определить для линейной модели, какие признаки являются самыми важными?
- наибольшим модулем соответствующего параметра линейной модели
- \(t\) -статистика \[ t(j) = \frac{|\mu_+ - \mu_-|}{\sqrt{\frac{n_+ \sigma^2_+ + n_- \sigma^2_-}{n_+ + n_-}}} \]
- исключаем по очереди один из признаков и смотрим, как это влияет на качество. Удаляем признаки таким жадным способом, пока не окажется выполненным некоторое условие (количество признаков или ухудшение качества).
- Можно использовать L1-регуляризацию, которая занулит веса на самых бесполезных признаках.
- Можно, в конце концов, посчитать корреляцию таргета и признака.
28. Опишите жадный алгоритм обучения решающего дерева.
Опишем базовый жадный алгоритм построения бинарного решающего дерева. Начнем со всей обучающей выборки \(X\) и найдем наилучшее ее разбиение на две части \(R_1(j, t) = \{x | x_j < t\}\) и \(R_2(j, t) = \{x | x_j \geq t\}\) с точки зрения заранее заданного функционала качества \(Q(X, j, t)\). Найдя наилучшие значения \(j\) и \(t\), создадим корневую вершину дерева, поставив ей в соответствие предикат \([x_j < t]\). Объекты разобьются на две части – одни попадут в левое поддерево, другие в правое. Для каждой из этих подвыборок рекурсивно повторим процедуру, построив дочерние вершины для корневой, и так далее. В каждой вершине мы проверяем, не выполнилось ли некоторое условие останова – и если выполнилось, то прекращаем рекурсию и объявляем эту вершину листом. Когда дерево построено, каждому листу ставится в соответствие ответ. В случае с классификацией это может быть класс, к которому относится больше всего объектов в листе, или вектор вероятностей (скажем, вероятность класса может быть равна доле его объектов в листе). Для регрессии это может быть среднее значение, медиана или другая функция от целевых переменных объектов в листе. Выбор конкретной функции зависит от функционала качества в исходной задаче.
29. Почему с помощью бинарного решающего дерева можно достичь нулевой ошибки на обучающей выборке без повторяющихся объектов?
Для выборки без повторяющихся объектов мы можем построить такое дерево, что количество листов в нем будет равно количеству объектов в выборке, и в каждом листе будет стоять отдельный объект. У каждого объекта будет уникальное признаковое описание, а значит, мы можем построить дерево предикатов так, чтобы оно делило выборку идеально. Само собой, обобщающая способность такого дерева будет не очень хорошей.
30. Как в общем случае выглядит критерий хаотичности? Как он используется для выбора предиката во внутренней вершине решающего дерева? Как вывести критерий Джини и энтропийный критерий?
Общий случай
\[ H( R) = \min_{c \in \mathbb{Y}} \frac{1}{|R|} \sum_{(x_i, y_i) \in R} L(y_i, c), \] Т.е. критерий показывает, насколько хорошо целевая переменная в данном множестве приближается константой. Чем менее разнообразно значение целевой переменной среди объектов, тем меньше значение критерия - поэтому мы пытаемся его минимизировать. При этом в процессе разбиения мы пытаемся максимизировать такой функционал: \[ Q(R_m, j, s)=H(R_m)-\frac{|R_\ell|}{|R_m|}H(R_\ell)-\frac{|R_r|}{|R_m|}H(R_r) \]
Джини
Рассмотрим ситуацию, в которой мы выдаём в вершине не один класс, а распределение на всех классах \(c = (c_1, \dots, c_K)\), \(\sum_{k = 1}^{K} c_k = 1\). Качество такого распределения можно измерять, например, с помощью критерия Бриера (Brier score): \[ H( R) = \min_{\sum_k c_k = 1} \frac{1}{|R|} \sum_{(x_i, y_i) \in R} \sum_{k = 1}^{K} (c_k - [y_i = k])^2. \] Легко заметить, что здесь мы, по сути, ищем каждый \(c_k\) как оптимальную с точки зрения MSE константу, приближающую индикаторы попадания объектов выборки в класс \(k\). Это означает, что оптимальный вектор вероятностей состоит из долей классов \(p_k\): \[c_* = (p_1, \dots, p_K)\] Если подставить эти вероятности в исходный критерий информативности и провести ряд преобразований, то мы получим критерий Джини: \[H( R)=\sum_{k = 1}^{K}p_k (1 - p_k).\]
Энтропийный
Мы уже знакомы с более популярным способом оценивания качества вероятностей – логарифмическими потерями, или логарифмом правдоподобия: \[ H( R)=\min_{\sum_k c_k = 1} \left(-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}\sum_{k = 1}^{K}[y_i = k]\log c_k\right) \] Для вывода оптимальных значений \(c_k\) вспомним, что все значения \(c_k\) должны суммироваться в единицу. Как известного из методов оптимизации, для учёта этого ограничения необходимо искать минимум лагранжиана: \[ L(c, \lambda)=-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}\sum_{k = 1}^{K}[y_i = k]\log c_k+\lambda\sum_{k = 1}^{K}c_k\to\min_{c_k} \] Дифференцируя, получаем: \[ \frac{\partial}{\partial c_k}L(c, \lambda)=-\frac{1}{|R|}\sum_{(x_i, y_i) \in R}[y_i = k]\frac{1}{c_k}+\lambda=-\frac{p_k}{c_k}+\lambda=0 \] откуда выражаем \(c_k = p_k / \lambda\). Суммируя эти равенства по \(k\), получим \[ 1 = \sum_{k = 1}^{K} c_k = \frac{1}{\lambda} \sum_{k = 1}^{K} p_k = \frac{1}{\lambda}, \] откуда \(\lambda = 1\). Значит, минимум достигается при \(c_k = p_k\), как и в предыдущем случае. Подставляя эти выражения в критерий, получим, что он будет представлять собой энтропию распределения классов: \[H( R)=-\sum_{k = 1}^{K}p_k\log p_k.\] Из теории вероятностей известно, что энтропия ограничена снизу нулем, причем минимум достигается на вырожденных распределениях (\(p_i = 1\), \(p_j = 0\) для \(i \neq j\)). Максимальное же значение энтропия принимает для равномерного распределения. Отсюда видно, что энтропийный критерий отдает предпочтение более распределениям классов в вершине.
31. Для какой ошибки строится разложение на шум, смещение и разброс? Запишите формулу этой ошибки.
Разложение ошибки на три компоненты, которое мы только что вывели, верно только для квадратичной функции потерь. Существуют более общие формы этого разложения, которые состоят из трёх компонент с аналогичным смыслом, поэтому можно утверждать, что для большинства распространённых функций потерь ошибка метода обучения складывается из шума, смещения и разброса; значит, и дальнейшие рассуждения про изменение этих компонент в композициях также можно обобщить на другие функции потерь (например, на индикатор ошибки классификации).
BVD для среднеквадратичного риска метода \(\mu\) (обученного на выборке \(X\)), усредненного по всем возможным выборкам. \[ L(\mu)= \mathbb{E}_{X} \Bigl[ \mathbb{E}_{x, y} \Bigl[ \bigl( y - \mu(X)(x) \bigr)^2 \Bigr] \Bigr] \] \[ L(\mu)= \underbrace{\mathbb{E}_{x, y}\Bigl[\bigl(y - \mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{шум}}+ \underbrace{\mathbb{E}_{x} \Bigl[\bigl(\mathbb{E}_{X} \bigl[ \mu(X) \bigr]-\mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{смещение}} +\underbrace{\mathbb{E}_{x} \Bigl[\mathbb{E}_{X} \Bigl[\bigl(\mu(X)-\mathbb{E}_{X} \bigl[ \mu(X) \bigr]\bigr)^2\Bigr]\Bigr]}_{\text{разброс}}. \]
32. Запишите формулы для шума, смещения и разброса метода обучения для случая квадратичной функции потерь.
\[ L(\mu)= \underbrace{\mathbb{E}_{x, y}\Bigl[\bigl(y - \mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{шум}}+ \underbrace{\mathbb{E}_{x} \Bigl[\bigl(\mathbb{E}_{X} \bigl[ \mu(X) \bigr]-\mathbb{E}[y | x]\bigr)^2\Bigr]}_{\text{смещение}} +\underbrace{\mathbb{E}_{x} \Bigl[\mathbb{E}_{X} \Bigl[\bigl(\mu(X)-\mathbb{E}_{X} \bigl[ \mu(X) \bigr]\bigr)^2\Bigr]\Bigr]}_{\text{разброс}}. \]
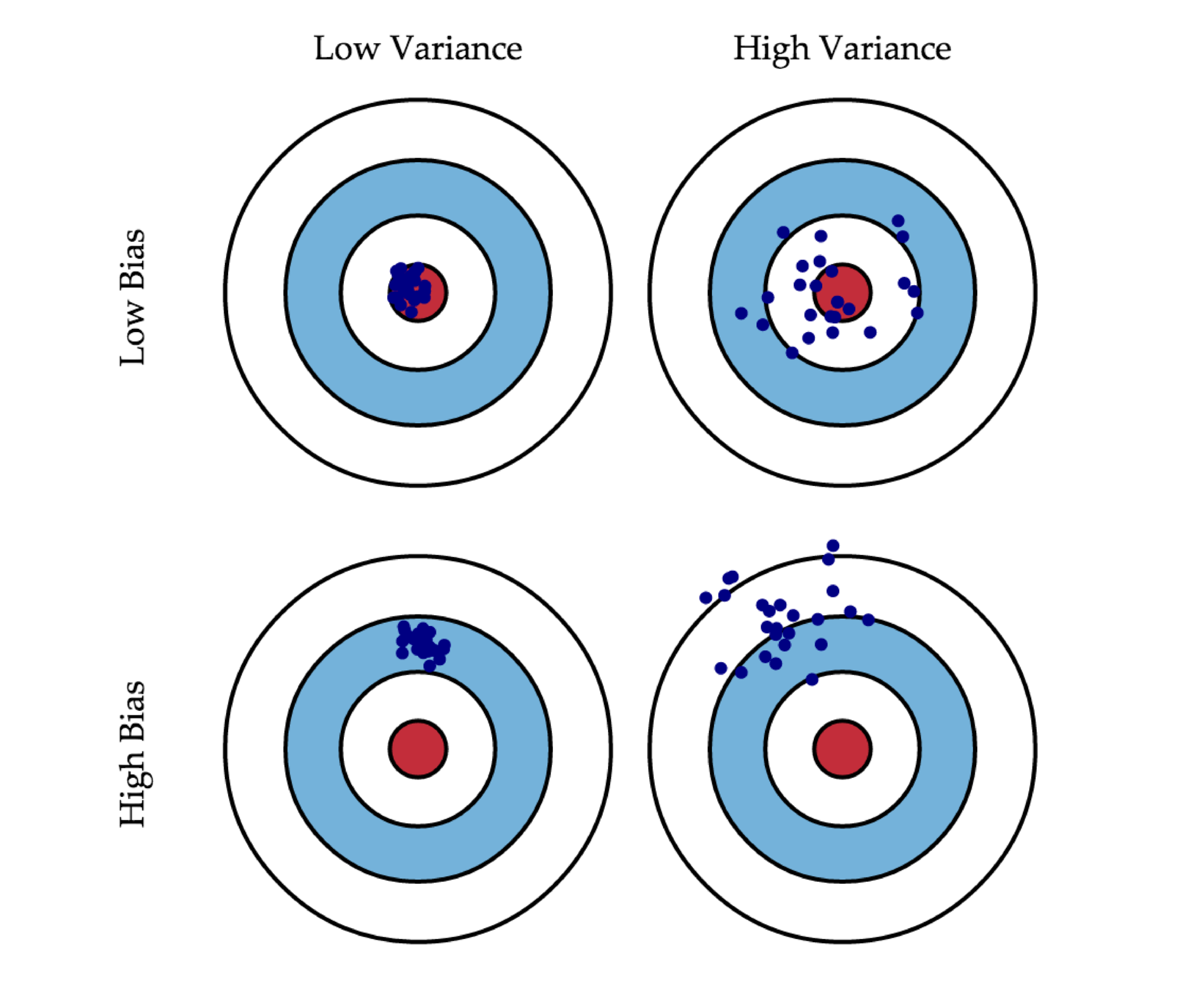
33. Приведите пример семейства алгоритмов с низким смещением и большим разбросом; семейства алгоритмов с большим смещением и низким разбросом. Поясните примеры.
Смещение показывает, насколько хорошо с помощью данных метода обучения и семейства алгоритмов можно приблизить оптимальный алгоритм. Как правило, смещение маленькое у сложных (precision) семейств (например, у деревьев) и большое у простых семейств (например, линейных классификаторов). Дисперсия показывает, насколько сильно может изменяться ответ обученного алгоритма в зависимости от выборки иными словами, она характеризует чувствительность метода обучения к изменениям в выборке. Как правило, простые семейства имеют маленькую дисперсию (variance), а сложные семейства большую дисперсию.
34. Что такое бэггинг? Как его смещение и разброс связаны со смещением и разбросом базовых моделей?
Для начала, бутстрап – способ ресэмплинга. По имеющейся выборке \(X\) создадим \(N\) новых выборок путем взятия элементов из \(X\) с повторениями.
Пусть имеется некоторый метод обучения \(\mu(X)\). Построим на его основе метод \(\tilde \mu(X)\), который генерирует случайную подвыборку \(\tilde X\) с помощью бутстрапа и подает ее на вход метода \(\mu\): \(\tilde \mu(X) = \mu(\tilde X)\). Напомним, что бутстрап представляет собой сэмплирование \(\ell\) объектов из выборки с возвращением, в результате чего некоторые объекты выбираются несколько раз, а некоторые – ни разу. Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте – соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
В бэггинге (bagging, bootstrap aggregation) предлагается обучить некоторое число алгоритмов \(b_n(x)\) с помощью метода \(\tilde \mu\), и построить итоговую композицию как среднее данных базовых алгоритмов: \[ a_N(x) = \frac{1}{N} \sum_{n = 1}^{N} b_n(x) = \frac{1}{N} \sum_{n = 1}^{N} \tilde \mu(X)(x). \] Такая композиция и называется бэггингом. Он позволяет объединить базовые алгоритмы с низким смещением, но высоким разбросом, в композицию с низким смещением и разбросом, причем, в идеальном случае (модели совсем не коррелируют) разброс падает в N раз. Если же корреляция имеет место, то уменьшение дисперсии может быть гораздо менее существенным.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
35. Что такое случайный лес? Чем он отличается от бэггинга над решающими деревьями?
Случайный лес - метод построения композиции, основанный на бэггинге над деревьями. Т.к. Бэггинг сильнее понижает разброс при слабой корреляции моделей, в RF предлагается специально ее понижать с помощью
- рандомизации по признакам (для каждого базового алгоритма используется некое подмножество признаков вместо всех) (это отличие от бэггинга над деревьями)
- рандомизации по объектам (для каждого базового алгоритма в бутстрапе используется не вся выборка X, а какая-то подвыборка)
36. Что такое out-of-bag оценка в бэггинге?
Мы можем для каждого объекта \(x_{i}\) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку
Каждое дерево в случайном лесе обучается по подмножеству объектов. Это значит, что те объекты, которые не вошли в бутстрапированную выборку \(X_n\) дерева \(b_n\), по сути являются контрольными для данного дерева. Значит, мы можем для каждого объекта \(x_i\) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку:
\[ \text{OOB} = \sum_{i = 1}^{\ell} L \left( y_i, \frac{1}{\sum_{n = 1}^{N} [x_i \notin X_n]} \sum_{n = 1}^{N} [x_i \notin X_n] b_n(x_i) \right), \] где \(L(y, z)\) – функция потерь. Можно показать, что по мере увеличения числа деревьев \(N\) данная оценка стремится к leave-one-out-оценке, но при этом существенно проще для вычисления.
37. Запишите вид композиции, которая обучается в градиентном бустинге. Как выбирают количество базовых алгоритмов в ней?
\(a_{N}(x)=\sum\limits_{n=0}^{N}\gamma_{n}b_{n}(x)\) В такой композиции каждый следующий базовый алгоритм исправляет ошибки предыдущего. При большом их числе мы начинаем переобучаться - можем использовать валидационную выборку для подбора (это просто гиперпараметр).
38. Что такое сдвиги в градиентном бустинге? Как они вычисляются и для чего используются?
Сдвиг (остаток) - расстояния от ответа нашего алгоритма до истинного ответа. \[ s_i^{(N)}=y_i - \sum_{n = 1}^{N - 1} b_n(x_i)=y_i- a_{N - 1}(x_i),\qquad i = 1, \dots, \ell \] Или \[ s_i=-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N - 1}(x_i)} \] С помощью сдвига мы настраиваем очередной базовой алгоритм: \[ b_N(x) := \mathop{\rm arg\,min}\limits_{b \in \mathbb{A}} \frac12 \sum_{i = 1}^{\ell} (b(x_i) - s_i^{(N)})^2 \]
39. Как обучается очередной базовый алгоритм в градиентном бустинге? Что такое сокращение шага?
Пусть мы построили композицию \(a_{N-1}(x)\) из \(N-1\) базовых алгоритмов. Хотим выбрать такой алгоритм следующим, чтобы как можно сильнее уменьшить ошибку
Допустим, мы построили композицию \(a_{N - 1}(x)\) из \(N - 1\) алгоритма, и хотим выбрать следующий базовый алгоритм \(b_N(x)\) так, чтобы как можно сильнее уменьшить ошибку: \[ \sum_{i = 1}^{\ell}L(y_i, a_{N - 1}(x_i) + \gamma_N b_N(x_i))\to\min_{b_N, \gamma_N} \]
Ответим в первую очередь на следующий вопрос: если бы в качестве алгоритма \(b_{N}(x)\) мы могли выбрать совершенно любую функцию, то какие значения ей следовало бы принимать на объектах обучающей выборки? Иными словами, нам нужно понять, какие числа \(s_1, \dots, s_\ell\) надо выбрать для решения следующей задачи: \[ \sum_{i = 1}^{\ell}L(y_i, a_{N - 1}(x_i) + s_i)\to\min_{s_1, \dots, s_\ell} \] Понятно, что можно требовать \(s_i = y_i - a_{N - 1}(x_i)\), но такой подход никак не учитывает особенностей функции потерь \(L(y, z)\) и требует лишь точного совпадения предсказаний и истинных ответов. Более разумно потребовать, чтобы сдвиг \(s_i\) был противоположен производной функции потерь в точке \(z = a_{N - 1}(x_i)\): \[ s_i=-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N - 1}(x_i)} \] В этом случае мы сдвинемся в сторону скорейшего убывания функции потерь. Заметим, что вектор сдвигов \(s = (s_1, \dots, s_\ell)\) совпадает с антиградиентом: \[ \left(-\left.\frac{\partial L}{\partial z}\right|_{z = a_{N - 1}(x_i)}\right)_{i = 1}^{\ell}=-\nabla_z\sum_{i = 1}^{\ell}L(y_i, z_i)\big|_{z_i = a_{N - 1}(x_i)} \] При таком выборе сдвигов \(s_i\) мы, по сути, сделаем один шаг градиентного спуска, двигаясь в сторону наискорейшего убывания ошибки на обучающей выборке. Отметим, что речь идет о градиентном спуске в \(\ell\) -мерном пространстве предсказаний алгоритма на объектах обучающей выборки. Поскольку вектор сдвига будет свой на каждой итерации, правильнее обозначать его как \(s_i^{(N)}\), но для простоты будем иногда опускать верхний индекс. Итак, мы поняли, какие значения новый алгоритм должен принимать на объектах обучающей выборки. По данным значениям в конечном числе точек необходимо построить функцию, заданную на всем пространстве объектов. Это классическая задача обучения с учителем, которую мы уже хорошо умеем решать. Один из самых простых функционалов – среднеквадратичная ошибка. Воспользуемся им для поиска базового алгоритма, приближающего градиент функции потерь на обучающей выборке: \[ b_N(x)=\mathop{\rm arg\,min}\limits_{b \in \mathbb{A}}\sum_{i = 1}^{\ell}\left(b(x_i) - s_i\right)^2 \] Отметим, что здесь мы оптимизируем квадратичную функцию потерь независимо от функционала исходной задачи – вся информация о функции потерь \(L\) находится в антиградиенте \(s_i\), а на данном шаге лишь решается задача аппроксимации функции по \(\ell\) точкам. Разумеется, можно использовать и другие функционалы, но среднеквадратичной ошибки, как правило, оказывается достаточно. Ещё одна причина для использования среднеквадратичной ошибки состоит в том, что от алгоритма требуется как можно точнее приблизить направление наискорейшего убывания функционала (то есть направление \((s_i)_i\)); совпадение направлений вполне логично оценивать через косинус угла между ними, который напрямую связан со среднеквадратичной ошибкой.
После того, как новый базовый алгоритм найден, можно подобрать коэффициент при нем по аналогии с наискорейшим градиентным спуском: \[ \gamma_N=\mathop{\rm arg\,min}\limits_{\gamma \in \mathbb{R}}\sum_{i = 1}^{\ell}L(y_i, a_{N - 1}(x_i) + \gamma b_N(x_i)) \] Описанный подход с аппроксимацией антиградиента базовыми алгоритмами и называется градиентным бустингом. Данный метод представляет собой поиск лучшей функции, восстанавливающей истинную зависимость ответов от объектов, в пространстве всех возможных функций. Ищем мы данную функцию с помощью спуска – каждый шаг делается вдоль направления, задаваемого некоторым базовым алгоритмом. При этом сам базовый алгоритм выбирается так, чтобы как можно лучше приближать антиградиент ошибки на обучающей выборке.
Сокращение шага - вместо перехода в оптимальную точку делаем укороченный шаг. По сути, мы снижаем доверие к каждому базовому алгоритму. \(\eta \in (0, 1]\) \(a_{N}(x)=a_{N-1}(x)+\eta\gamma_{N}b_{N}(x)\)
40. В чём заключается переподбор прогнозов в листьях решающих деревьев в градиентном бустинге?
Вспомним, что решающее дерево разбивает все пространство на непересекающиеся области,в каждой из которых его ответ равен константе: \[ b_n(x)=\sum_{j = 1}^{J_n}b_{nj}[x \in R_j], \] где \(j = 1, \dots, J_n\) – индексы листьев, \(R_j\) – соответствующие области разбиения, \(b_{nj}\) – значения в листьях. Значит, на \(N\) -й итерации бустинга композиция обновляется как \[ a_N(x)=a_{N - 1}(x)+\gamma_N\sum_{j = 1}^{J_N}b_{Nj}[x \in R_j]=a_{N - 1}(x)+\sum_{j = 1}^{J_N}\gamma_Nb_{Nj}[x \in R_j]. \] Видно, что добавление в композицию одного дерева с \(J_N\) листьями равносильно добавлению \(J_N\) базовых алгоритмов, представляющих собой предикаты вида \([x \in R_j]\). Если бы вместо общего коэффициента \(\gamma_N\) был свой коэффициент \(\gamma_{Nj}\) при каждом предикате, то мы могли бы его подобрать так, чтобы повысить качество композиции. Если подбирать свой коэффициент \(\gamma_{Nj}\) при каждом слагаемом, то потребность в \(b_{Nj}\) отпадает, его можно просто убрать: \[ \sum_{i = 1}^{\ell}L\left(y_i,a_{N - 1}(x_i)+\sum_{j = 1}^{J_N}\gamma_{Nj}[x \in R_j]\right)\to\min_{\{\gamma_{Nj}\}_{j = 1}^{J_N}}. \] Поскольку области разбиения \(R_j\) не пересекаются, данная задача распадается на \(J_N\) независимых подзадач: \[ \gamma_{Nj}=\mathop{\rm arg\,min}\limits_\gamma\sum_{x_i \in R_j}L(y_i, a_{N - 1}(x_i) + \gamma),\qquad j = 1, \dots, J_N. \]
41. Как в xgboost выводится функционал ошибки с помощью разложения в ряд Тейлора?
Мы хотим найти алгоритм \(b(x)\), решающий следующую задачу: \[ \sum_{i = 1}^{\ell} L(y_i, a_{N - 1}(x_i) + b(x_i)) \to \min_{b} \] Разложим функцию \(L\) в каждом слагаемом в ряд Тейлора до второго члена с центром в ответе композиции \(a_{N - 1}(x_i)\): \[ \sum_{i = 1}^{\ell}L(y_i, a_{N - 1}(x_i) + b(x_i))\approx \sum_{i = 1}^{\ell} \left(L(y_i, a_{N - 1}(x_i))-s_i b(x_i)+\frac12h_i b^2(x_i)\right), \] где через \(h_i\) обозначены вторые производные по сдвигам: \[ h_i = \left. \frac{\partial^2}{\partial z^2} L(y_i, z) \right|_{a_{N - 1}(x_i)} \] Первое слагаемое не зависит от нового базового алгоритма, и поэтому его можно выкинуть. Получаем функционал: \[ \sum_{i = 1}^{\ell} \left(-s_i b(x_i)+\frac{1}{2}h_i b^2(x_i)\right)\to\min_{b} \]
Покажем, что он очень похож на среднеквадратичный из формулы. Преобразуем его: \[ \sum_{i = 1}^{\ell}\left(b(x_i) - s_i\right)^2\\ = \sum_{i = 1}^{\ell} \left(b^2(x_i)-2 s_i b(x_i)+s_i^2\right) = \{\text{последнее слагаемое не зависит от $b$}\} \\ = \sum_{i = 1}^{\ell} \left(b^2(x_i)-2 s_i b(x_i)\right)\\ = 2\sum_{i = 1}^{\ell}\left(-s_ib(x_i)+\frac{1}{2}b^2(x_i)\right) \to\min_{b} \] Видно, что последняя формула совпадает с точностью до константы, если положить \(h_i = 1\). Таким образом, в обычном градиентном бустинге мы используем аппроксимацию второго порядка при обучении очередного базового алгоритма, и при этом отбрасываем информацию о вторых производных (то есть считаем, что функция имеет одинаковую кривизну по всем направлениям).
42. Какие регуляризации используются в xgboost?
Будем далее работать с функционалом. Он измеряет лишь ошибку композиции после добавления нового алгоритма, никак при этом не штрафуя за излишнюю сложность этого алгоритма. Ранее мы решали проблему переобучения путем ограничения глубины деревьев, но можно подойти к вопросу и более гибко. Мы выясняли, что дерево \(b(x)\) можно описать формулой \[ b(x) = \sum_{j = 1}^{J} b_{j} [x \in R_{j}] \] Его сложность зависит от двух показателей:
- Число листьев \(J\). Чем больше листьев имеет дерево, тем сложнее его разделяющая поверхность, тем больше у него параметров и тем выше риск переобучения.
- Норма коэффициентов в листьях \(\|b\|_2^2 = \sum_{j = 1}^{J} b_j^2\). Чем сильнее коэффициенты отличаются от нуля, тем сильнее данный базовый алгоритм будет влиять на итоговый ответ композиции.
Добавляя регуляризаторы, штрафующие за оба этих вида сложности, получаем следующую задачу: \[ \sum_{i = 1}^{\ell} \left(-s_i b(x_i)+\frac{1}{2}h_i b^2(x_i)\right) +\gamma J +\frac{\lambda}{2}\sum_{j = 1}^{J}b_j^2 \to\min_{b} \] Если вспомнить, что дерево \(b(x)\) дает одинаковые ответы на объектах, попадающих в один лист, то можно упростить функционал: \[ \sum_{j = 1}^{J} \Biggl\{ \underbrace{ \Biggl(-\sum_{i \in R_j} s_i\Biggr) }_{=-S_j} b_j+\frac12 \Biggl(\lambda+ \underbrace{\sum_{i \in R_j} h_i}_{=H_j} \Biggr) b_j^2+\gamma \Biggr\} \to \min_{b} \] Каждое слагаемое здесь можно минимизировать по \(b_j\) независимо. Заметим, что отдельное слагаемое представляет собой параболу относительно \(b_j\), благодаря чему можно аналитически найти оптимальные коэффициенты в листьях: \[ b_j = \frac{S_j}{H_j + \lambda} \] Подставляя данное выражение обратно в функционал, получаем, что ошибка дерева с оптимальными коэффициентами в листьях вычисляется по формуле \[ H(b)= -\frac12\sum_{j = 1}^{J} \frac{S_j^2}{H_j + \lambda}+\gamma J \]
43. Задача кластеризации. Метрики качества.
Приведём несколько примеров внутренних метрик качества. Будем считать, что каждый кластер характеризуется своим центром \(c_k\).
Внутрикластерное расстояние
\[ \sum_{k = 1}^{K}\sum_{i = 1}^{\ell}[a(x_i) = k]\rho(x_i, c_k), \] где \(\rho(x, z)\) – некоторая функция расстояния. Данный функционал требуется минимизировать, поскольку в идеале все объекты кластера должны быть одинаковыми.
Межкластерное расстояние
\[ \sum_{i, j = 1}^{\ell}[a(x_i) \neq a(x_j)]\rho(x_i, x_j). \] Данный функционал нужно максимизировать, поскольку объекты из разных кластеров должны быть как можно менее похожими друг на друга.
Индекс Данна (Dunn Index)
\[ \frac{ \min_{1 \leq k < k^\prime \leq K}d(k, k^\prime) }{ \max_{1 \leq k \leq K}d(k) }, \] где \(d(k, k^\prime)\) – расстояние между кластерами \(k\) и \(k^\prime\) (например, евклидово расстояние между их центрами), а \(d(k)\) – внутрикластерное расстояние для \(k\) -го кластера (например, сумма расстояний от всех объектов этого кластера до его центра). Данный индекс необходимо максимизировать.
44. Метод K-Means, вывод его шагов.
Одним из наиболее популярных методов кластеризации является, который оптимизирует внутрикластерное расстояние, в котором используется квадрат евклидовой метрики.
Заметим, что в данном функционале имеется две степени свободы: центры кластеров \(c_k\) и распределение объектов по кластерам \(a(x_i)\). Выберем для этих величин произвольные начальные приближения, а затем будем оптимизировать их по очереди:
- Зафиксируем центры кластеров. В этом случае внутрикластерное расстояние будет минимальным, если каждый объект будет относиться к тому кластеру, чей центр является ближайшим: \[ a(x_i)=\mathop{\rm arg\,min}\limits_{1 \leq k \leq K}\rho(x_i, c_k). \]
- Зафиксируем распределение объектов по кластерам. В этом случае внутрикластерное расстояние с квадратом евклидовой метрики можно продифференцировать по центрам кластеров и вывести аналитические формулы для них: \[ c_k=\frac{1}{\sum_{i = 1}^{\ell} [a(x_i) = k]}\sum_{i = 1}^{\ell}[a(x_i) = k] x_i. \]
Повторяя эти шаги до сходимости, мы получим некоторое распределение объектов по кластерам. Новый объект относится к тому кластеру, чей центр является ближайшим.
Результат работы метода K-Means существенно зависит от начального приблжения. Существует большое количество подходов к инициализации; одним из наиболее успешных считается k-means++.